1. Introduction

把模型用在資源有限的環境下，擁有比較少量的參數，但是與原模型有差不多的效能

五個 network compression 技術（軟體導向）：

1. Network Pruning

2. Knowledge Distillation

3. Parameter Quantization

4. Architecture Design

5. Dynamic Computation

五種技術的前四種不互斥，可以同時使用

2. Network Pruning

network 中有許多參數，有可能有些參數沒有用處，只是佔空間、浪費運算資源而已，而 network pruning 就是把 network 中沒有用的參數找出來刪除掉

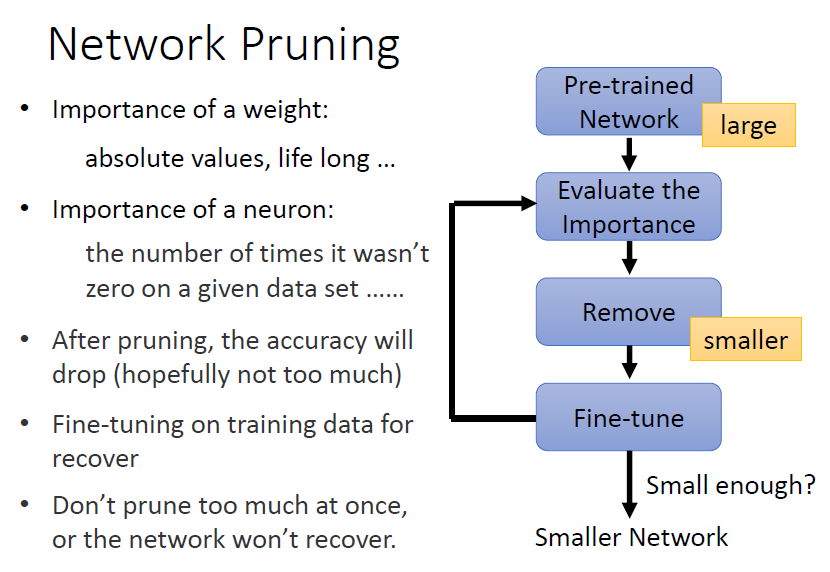
1. 訓練一個大的模型

2. 評估 weight 或 neuron 的重要性
   • weight 的重要性
     • 參數加上絕對值得大小
     • 套用 LLL 的思想，計算 $b_i$
   • neuron 的重要性
     • 計算神經元輸出不為 0 的次數

3. 移除不重要的 weight 或 neuron（此時模型性能可能下降）

4. 微調模型

5. 重複步驟 2. 至 4.

2.1 Weight pruning

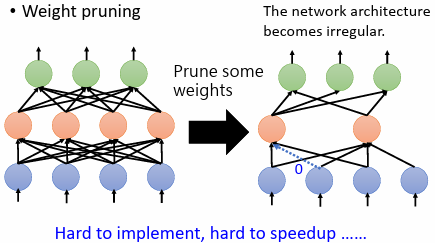
問題：

刪除 weight 後，神經網路形狀不規則，實作上難以實現，也難以使用 GPU 加速矩陣乘法

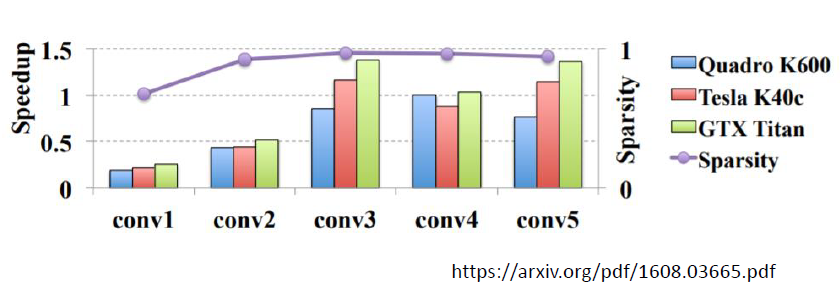
以上實驗結果顯示，即使剪掉 95% 的 weight，但是運算時大多時候並沒有變得更快

2.2 Neuron pruning

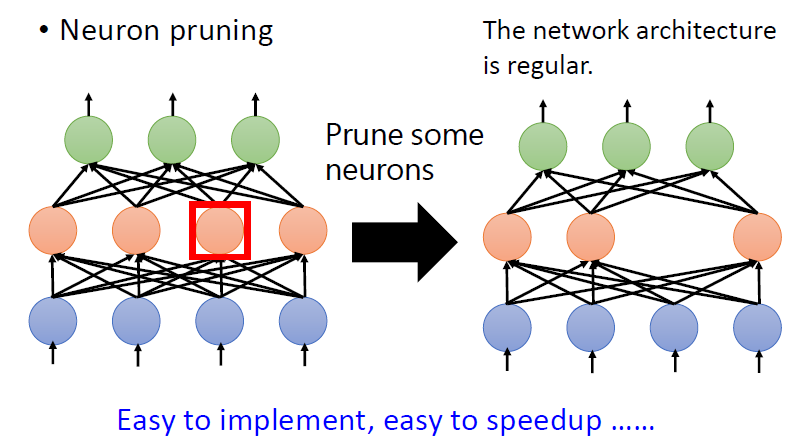
容易實現，且容易加速運算

2.3 Why Pruning？

問題：

先訓練大的 network 再把它變小，且希望小的 network 跟大的 network 正確率沒有差太多，那麽為什麽不直接訓練小的 network

原因：

因為大的 network 比較好訓練，可參照過去錄影：https://youtu.be/_VuWvQUMQVk

2.3.1 Lottery Ticket Hypothesis

Lottery Ticket Hypothesis 解釋為什麼大的 network 比較容易訓練（注意是”假說”）

大的 network 可以視為是很多小的 sub-network 的組合，當訓練大的 network 時，等於是在訓練很多小的 network

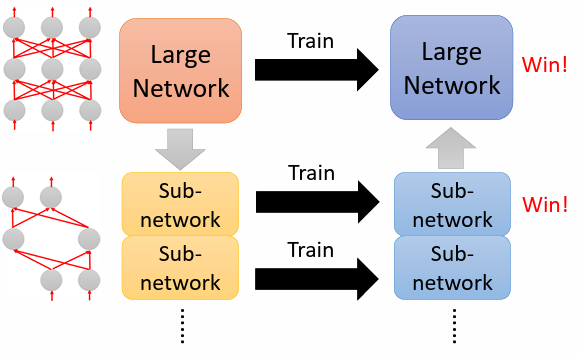
對於每個 sub-network 不一定可以訓練成功，不一定可以透過 gradient descent 找到好的解使 loss 變低。但只要有大量的 sub-network，其中一個成功，大的 network 就成功了

實驗證明：

將一參數是隨機初始化的大 network 訓練後進行 pruning 的到一個 pruned network

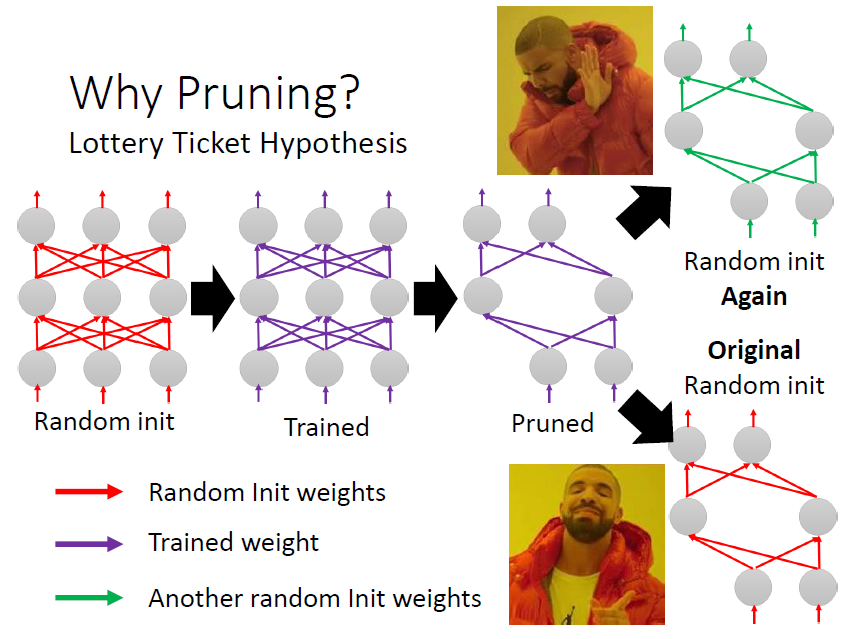
針對此 pruned network 分別採取兩個行為：

• 參數隨機初始化進行訓練，實驗結果發現難以訓練成功

• 參數使用 pruning 前且訓練前 network，實驗結果發現可以訓練成功

解構 Lottery Ticket Hypothesis：

結論：

• 找到了兩種最為有效的 pruning strategy

• 正負號是 network 能不能被訓練起來的關鍵，絕對值事實上相對不重要

• 隨機初始化 network，就已經可以對一些參數進行剪枝，並得到一個效果不錯的 network

2.3.2 反對大樂透假說：Rethinking the Value of Network Pruning

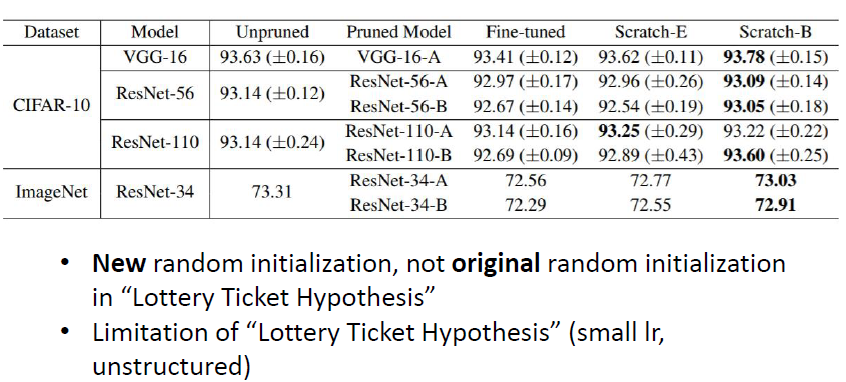
• 對於 pruned 後的 network，作完全隨機的初始化，並經過更多 epoch 的訓練，也更得到比 pruned 後的 network 甚至 pruned 前的 network 更好的性能

• 大樂透假說可能只在某些條件下才觀察得到
  • 小的 learning rate
  • 不規則的 network （刪除 weight）

3. Knowledge Distillation

對於同一個任務，訓練兩個 network：

• Teacher Network：大的 network，也可以是多個模型的 ensemble

• Student Network：小的 network，是真正想要訓練的 network

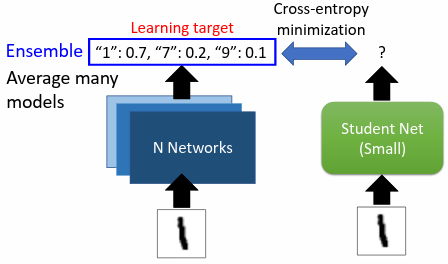
以手寫辨識為例，teacher network 輸出數字的機率分布，student network 的輸出也要是數字的機率分布，期望與 teacher network 的結果越接近越好

3.1 Temperature for softmax

輸出是經過 softmax 運算的結果，使每一個數字變為機率分布介於 0 和 1 之間

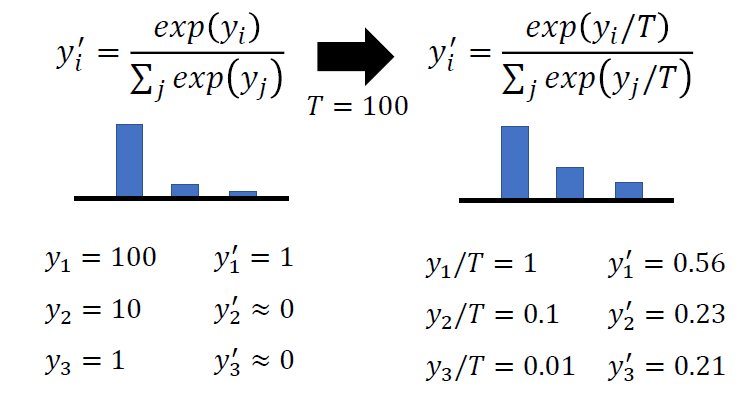
問題：

使用原始的 softmax 可能會有機率分布集中的問題，這樣與直接給予正確答案沒有什麼不同，對於 student network 來說沒有幫助，因為 teacher network 沒有提供額外的訊息

解決：

新增超參數 temperature $T$，使輸出的機率分布變得比較平滑

4. Parameter Quantization

4.1 減少 bits 數

使用較少的空間（bits）儲存一個參數。一般在存一個參數可能是用 64 bits，但可能不必用這麼高的精度，可能用 16 bits、8 bits 或更少就足夠了

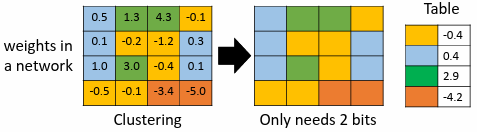
4.2 Weight clustering

依參數數值接近程度將參數分群，讓同一群的參數有一樣的數值（取同群參數的平均），並建立一個 table 記錄每一群的值

4.3 Huffman encoding

較常出現的使用較少 bits；較少出現的使用較多 bits

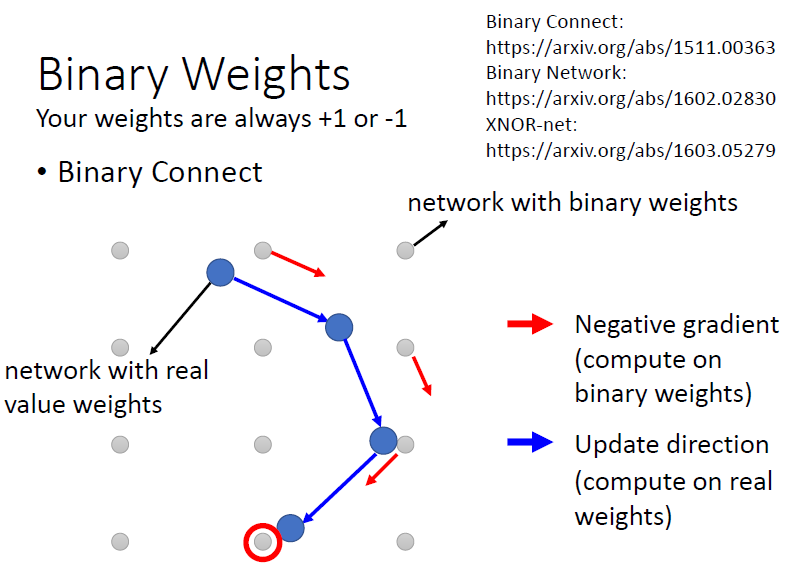
4.4 Binary weight

只以正負 1 表示所有參數

5. Architecture Design

5.1 Low rank approximation

輸入有 N 個 neuron，輸出有 M 個 neuron，兩層之間的參數量 W = N x M ，只要 N 跟 M 其中一者很大，W 的參數量就會很大

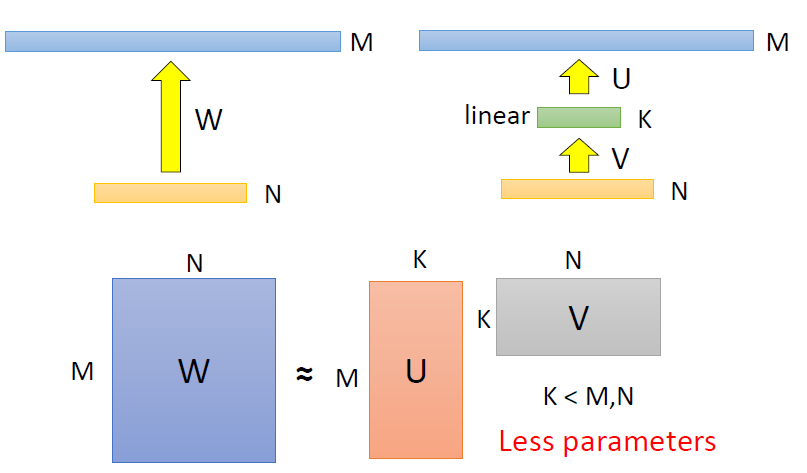
為了減少參數量，可在 N 跟 M 中間新增一層 layer，這一層的 neuron 數目是 K

原參數量是 M x N；而新增一 neuron 數為 K 的 layer 後，參數量減少為 K x（N + M），若 K 遠小於 M 跟 N，那麼 U 跟 V 的參數量加起來，會比 W 還少的多

問題：

W 分成用 U 跟 V 兩層來分開表示時，會減少 W 的可能性，W 的 rank 會 ≤ K

5.2 Depthwise Separable Convolution

5.2.1 Depthwise Convolution

考慮一個 channel 的內部關係

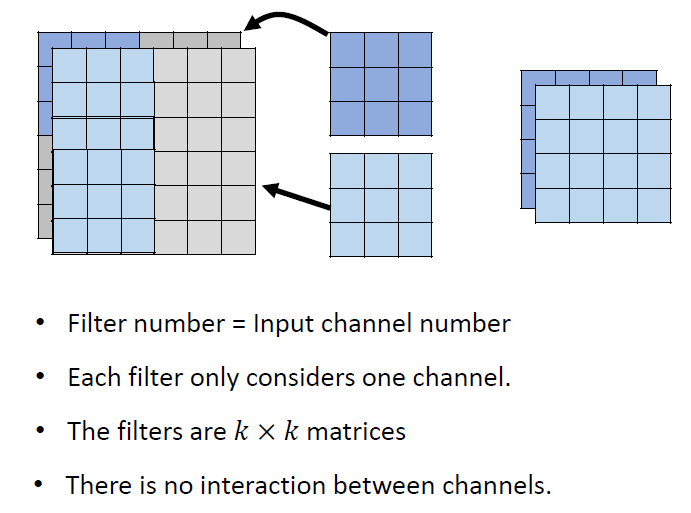
• 每個 filter 負責一個 channel

• channel 數目和 filter 數目相同

• input channel 和 output channel 數目相同

• channels 之間沒有互動

5.2.2 Pointwise Convolution

考慮 channels 之間的關係

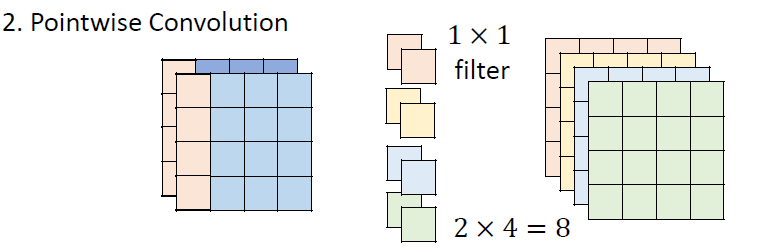
做完 depthwise convolution 後，進行 pointwise convolution

• filter size 限制為 $1\times1$

• 輸入 channel 和輸出 channel 的數目可以不同

二者關係：

觀察右側紅色左上角框內數據的來源，都是來自左側原圖中左上 $3\times3\times2$ 的區域，只是在 depthwise separable convolution中，將原來的一次卷積的操作改為兩次卷積，以此減少參數量

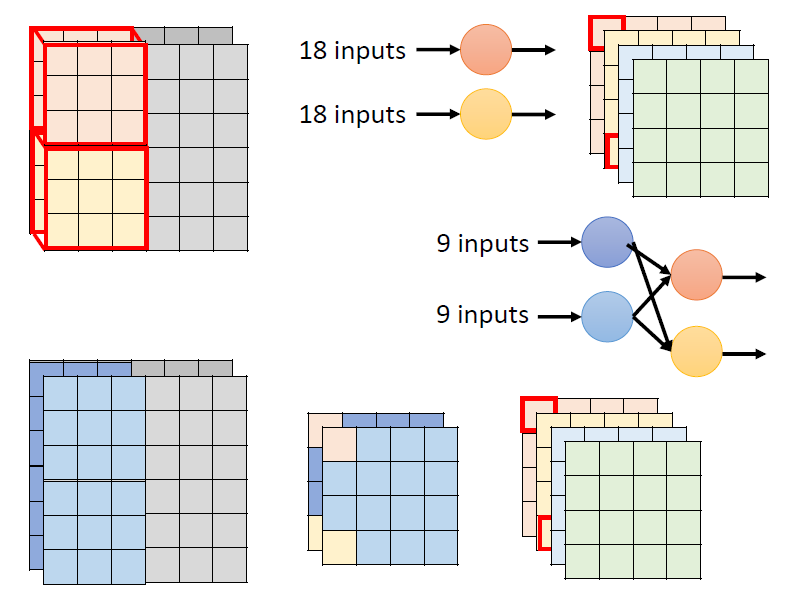
參數量變化：

實例：

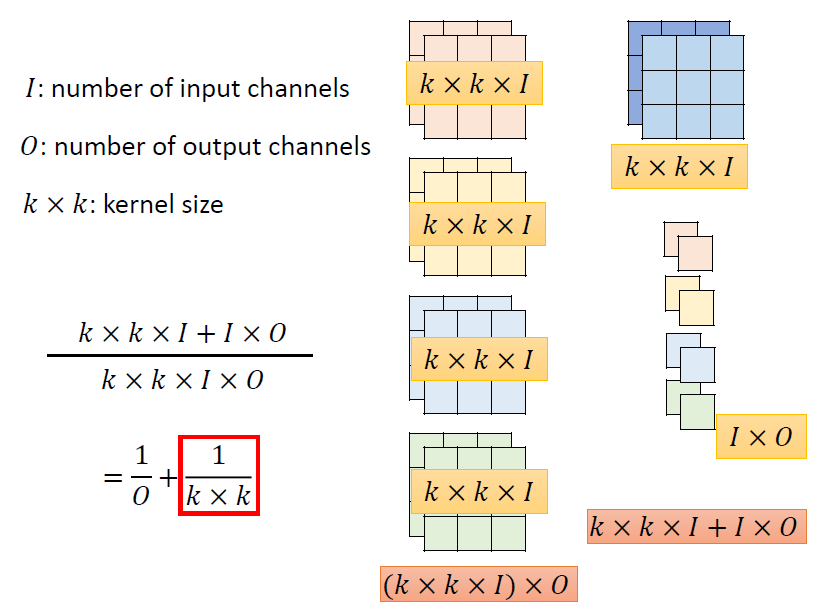
左側為一般的卷積需要的參數量；右邊是 depthwise separable convolution 需要的參數量

計算可得，兩者的參數量之比主要取決於 $\frac{1}{k\times k}$

5.3 To learn More

• SqueezeNet

• MobileNet

• ShuffleNet

• Xception

• GhostNet

6. Dynamic Computation

希望 network 可以根據實際運算資源情況，自動調整需要的運算量

6.1 Dynamic Depth

在 layers 間加上 extra layers，extra layers 根據每一個 hidden layers 的輸出，中途決定分類的結果

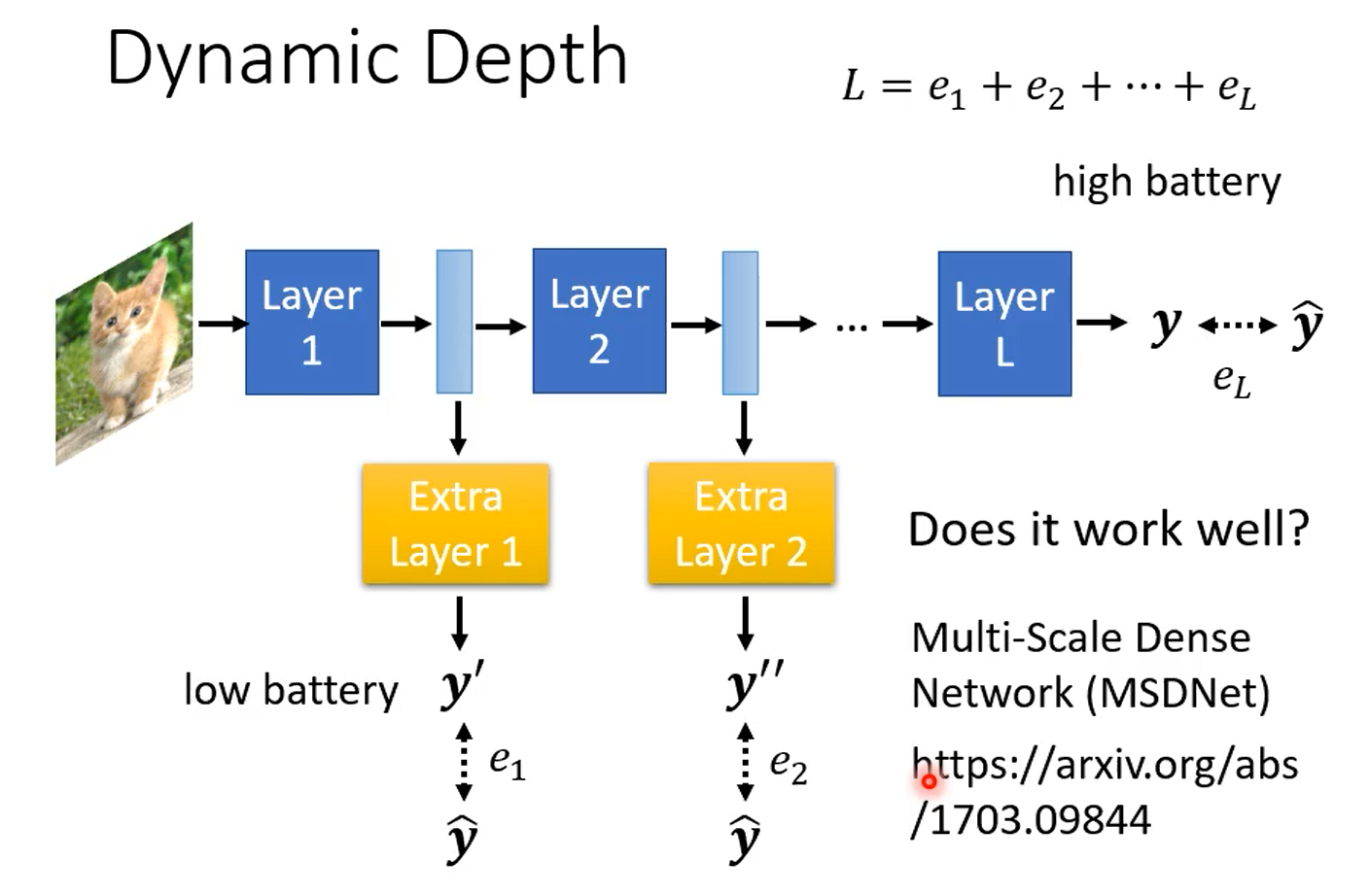
• 運算資源充足時，可讓圖片跑過所有的 layer，得到最終的分類結果

• 運算資源不足時，讓 network 決定要在哪一個 layer 自行做輸出

期望 ground truth 跟每一個 extra layer 的輸出越接近越好，因此把所有的輸出跟 ground truth 的 cross entropy 加總得到 $L$，目標最小化 $L$

其他方法可參考論文：Multi-Scale Dense Networks for Resource Efficient Image Classification（MSDNet）

6.2 Dynamic Width

在同一個 network 中，設定好幾個不同的寬度

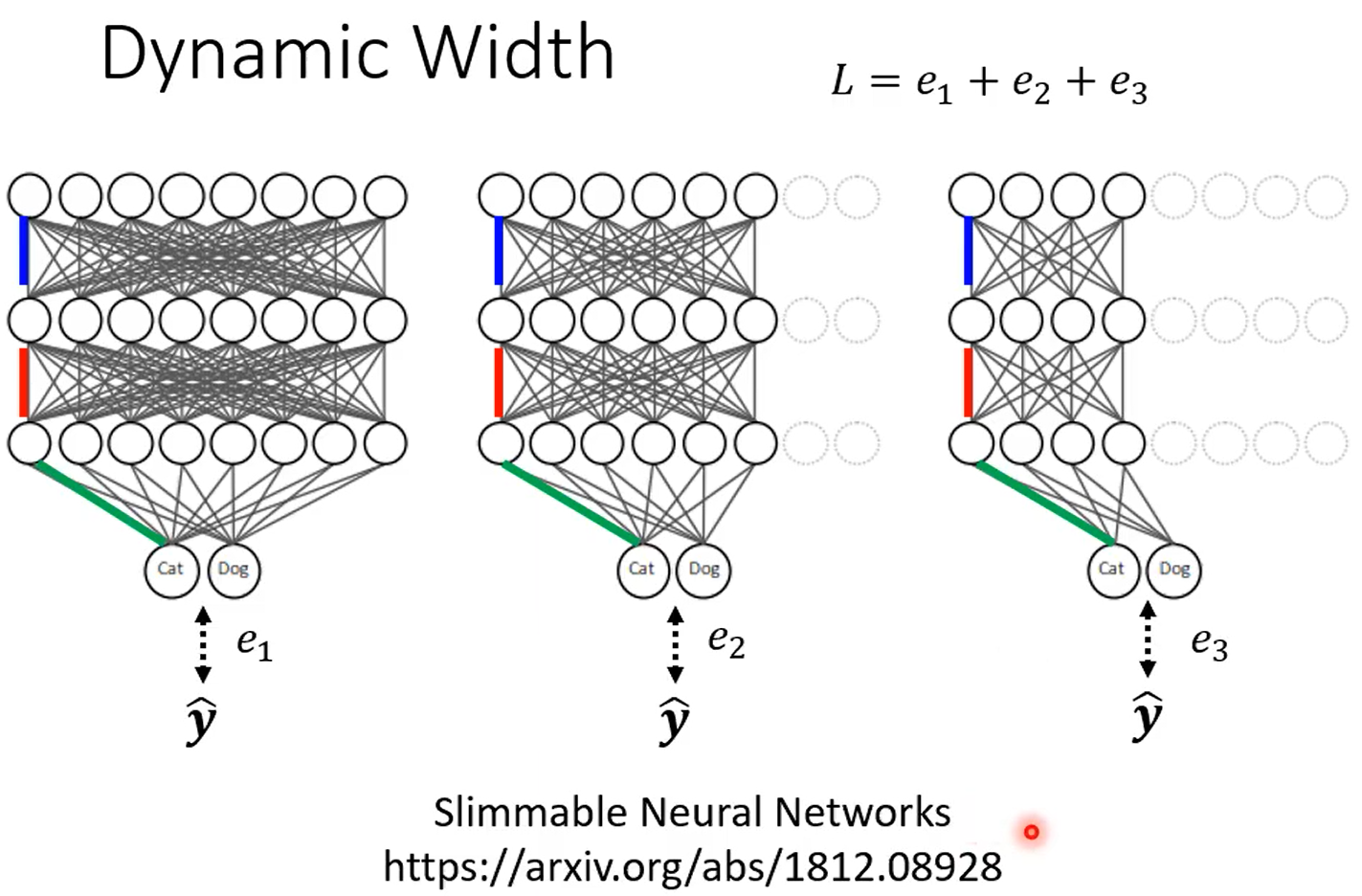
將不同寬度的 network 產生的每一個輸出跟 ground truth 的差距加總得到 $L$，目標最小化 $L$

6.3 network 自行決定深度和寬度

根據輸入資料的難易程度，讓 network 自行決定執行的寬度和深度

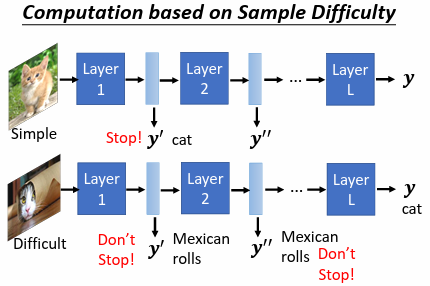
實現：

• SkipNet: Learning Dynamic Routing in Convolutional Networks

• Runtime Neural Pruning

• BlockDrop: Dynamic Inference Paths in Residual Networks